El camino - Adrián Paenza
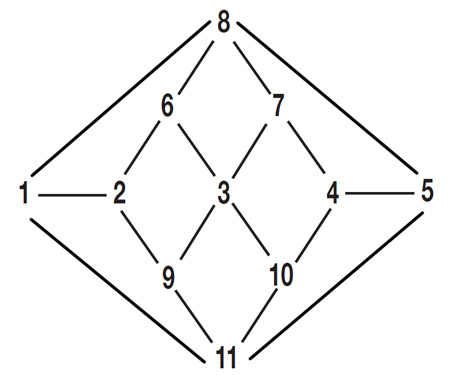
Para convencerse de que no existe (ni existirá) una solución al problema, le propongo que hagamos lo siguiente. Voy a poner un círculo alrededor de algunos números (ciudades) y a otros los voy a enmarcar en un cuadrado. ¿Cómo decidir a cuáles ponerles un círculo y a cuáles un cuadrado? Si dos números están conectados por un camino, entonces uno debe tener un círculo y el otro un cuadrado, o sea, tienen que tener dos figuras geométricas distintas alrededor. Por ejemplo, como le puse un círculo al 1, entonces el 2 (que está conectado con el 1) tiene que tener un cuadrado. Pero como el 2 tiene un cuadrado y está conectado tanto con el 6 como con el 9, entonces ambos tienen que tener un círculo. De la misma forma, el 3 y el 8 tienen que tener un círculo, porque están conectados con el 6 que tiene un cuadrado. Y así siguiendo. Más aún: le sugiero que tome la Figura 1 que está más arriba, en donde aparece el planteo del problema, y haga usted la distribución de los círculos y los cuadrados. Verá que obtiene el mismo resultado: tendrán círculos los números 1, 6, 7, 9, 10 y 5, mientras que quedarán con cuadrados el 2, 3, 4, 8 y 11. O al revés: quedarán con cuadrados alrededor el 1, 6, 7, 9, 10 y 5 mientras que tendrán un círculo el 2, 3, 4, 8 y 11. De acuerdo con lo que yo hice en la Figura 2, hay seis números que tienen círculos y cinco que tienen un cuadrado.
Dicho esto, quiero que pensemos juntos algo más que será muy importante: cada vez que caminamos de una ciudad a otra (o bien, de un número a otro), pasamos de un número que tiene un círculo a otro que tiene un cuadrado. O al revés. Es decir, vamos alternando números que tienen un círculo con números que tienen un cuadrado.
Ahora llegó el momento interesante en donde vamos a concluir que el camino que queremos construir no puede existir. ¿Por qué? Como el total de ciudades es 11, entonces usted tendrá que dar 11 pasos para recorrerlas todas y volver a la de partida. Es importante que me siga con este último argumento. Como usted empieza “parado” en algún número, tendrá que dar en total 11 pasos hasta volver al punto inicial (que le permitirá recorrer una vez por cada ciudad que no es la de partida, pero tendrá que volver al lugar inicial). Por eso son 11 pasos. Voy a llamar (CIR) a los números que tienen un círculo y (CUA) a los que tienen un cuadrado. Digamos que empieza parado en un número que tiene un círculo (CIR), cuando da el primer paso llega a un número (CUA). Cuando da el segundo paso llega a un número con un círculo (CIR), y al seguir caminando va alternando (CIR) con (CUA). Como escribí recién, uno tiene que dar en total once pasos.
Fíjese que cada vez que dio un número par de pasos llega a un (CIR). Cuando dio un número impar de pasos, llega a un número (CUA). Y eso debería ser suficiente para convencerla/o de que el camino no va a existir. ¿Quiere pensarlo usted en soledad?
Es que como tenemos que dar once pasos, que es un número impar de pasos y empezamos en un número (CIR), llegaríamos a uno que es (CUA), y eso demuestra que el camino que queremos construir no va a existir, porque el objetivo es llegar a la misma ciudad de partida pasando una sola vez por cada ciudad/número. Por lo tanto, no importa qué camino pretendamos construir, será imposible encontrarlo.
↓Figura 2 ↓